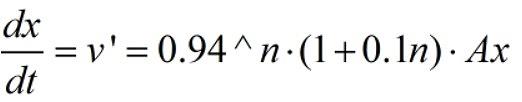作者：378330323

來源：戴森球計畫吧

蒸餾塔產重氫，0.01搖號概率，0.99的氫被淘汰，那產氫期望如何計算？

1個氫被1個塔淘汰的概率，是0.99；連續被2個塔淘汰的概率，是0.99^2；被n個塔淘汰的概率，是0.99^n

那麼，1個氫被其中任意1個塔搖號成功的概率，就是1-0.99^n

當皮帶跑起來，用黃帶（6/秒）、藍帶（12/秒）、綠帶（30/秒）

產出期望就是，（1-0.99^n）乘6、乘12、乘30。

哼，簡單的初中數學。

在全綠帶（30/秒）情況下，我excel一拉就是一整個表

注意到，串聯塔數在大於10、大於22的時候，產出速度就可以分別達到黃帶50%、100%的運量了。

知道這個有什麼用呢？

意思就是：

1．超過22個塔串聯（比如23個），你黃帶就爆炸，轉轉樂變成停停哭。

這裡要注意！！無論怎麼補氫，產出都不能讓帶子爆炸，只能無限接近。你問我為什麼？我的回答是，產出爆炸會導致某個塔產出堵塞，1個塔產出堵塞，整個串聯線一起遭殃，轉轉樂你怎麼了，你怎麼成停停哭了。

2．每10個塔再不補氫，你大概會淨虧1個塔的效率（ 22/2 – 10 = 1 ）。四捨五入就是一棟海景大別野。

3．硬串50個塔而不補氫，產出才能快要撐爆藍帶。而2個22塔串聯，就可以達到這個產量了（2個滿黃帶）。這一波啊，這一波淨虧6個塔。幾棟海景大別野了自己數數？

4．基於第3點，討論藍帶輸出、綠帶輸出，都可以簡化為討論黃帶輸出。畢竟藍、綠帶速都是黃帶的倍數，通過補氫、新拉一條線等手段，即可將藍、綠帶問題轉化為黃帶問題。

“好了，我知道了，我就10塔一補/22塔一補。”

不少吧友表示學到了。

一些更正和實驗

1．在這一章節，樓主把2、3級帶子顏色整串了，應當是2級綠帶、3級藍帶。但是2級帶、3級帶對應的速度沒有錯誤，所以資料也是正確的

下面就10塔一補、22塔一補作一些實驗驗證

2．10塔一補的實驗驗證

2．10塔一補的實驗驗證

10塔一補，聯夠20塔，即有344/m的速度。讓我們搭建起來康一康

可以看到，氫消耗/產出，基本在330-355之間，基本符合我們得到的資料表，10塔分產172*2=344/分的一個理論。

理論上，每10塔1補，那麼每20塔，就有約344/m的補氫輸入和重氫輸出（略小於360/m）；每40塔，有就688/m補氫輸入和重氫輸出（與720/m相差32/m）；每100塔，就有1721/m補氫輸入和重氫輸出(與1800/m相差79/m)。

3．22塔一補的實驗驗證

這個簡單，把10塔一補的補氫線拆掉，再額外搭2塔

產線啟動後已達到349/分↓，應該會無限接近於357/分的22塔串聯理論值 。

所以說，如果每22塔1補，那麼每22塔，就有約357/m的補氫輸入和重氫輸出（略小於360/m）；每44塔，有就714/m補氫輸入和重氫輸出（與720/m相差6/m）；每110塔，就有1785/m補氫輸入和重氫輸出(與1800/m相差15/m)。

4. 產線停滯的一個案例

在22塔實際測試中，啟動不久跑出了高於黃帶速度的405/分重氫資料↓

這個可以忽略，因為樓主啟動方式是22塔先滿載再轉轉樂，相當於啟動時臨時有22座1塔一補的蒸餾塔，其分產可達18 * 22 = 396/分的重氫產出。

但是一開局出現的多餘產出，引發了產物堆積導致的停轉，肯定會來臨。比如下圖

gif上傳大小有限，可以隱約看到，雖然當前分產，還是高於360/m，但上方最右已經產物堆積，上方傳送帶肉眼可見變得稀薄，右上二塔已經熄火

隨之而來的，就是整條線停產，直到右上堆積的產物被運出來。不止這些，這條產線如果再想啟動，需要重新補入氫原子，一邊補，一連產，要較久時間才能平衡回滿帶。

這就是產速超過帶速帶來的後果。

10塔1補、22塔1補，這個數量級還是比較美好的，串聯的不算多，補氫也不太頻繁，線路鋪設的工作量可以接受。

那麼像我們一般玩家，很隨意地每9台一補、每5台一補或者每13台一補的“感覺性”補氫方式，其提供的產重氫效率是多少呢？

那麼下面我們討論討論，“如果規律補氫，每n座塔一補，那我補多少次（設為m次），才能剛好不多於黃帶速度？”

（再次重申，為什麼要求不多於黃帶速度：無論怎麼補氫，產出都不能讓帶子爆炸，只能無限接近。產出爆炸會導致某個塔產出堵塞，1個塔產出堵塞，整個串聯線一起遭殃。）

好了，我現在是1塔一補。從已經得到的excel表上可知，1塔綠帶的產量是0.3/秒，要達到黃帶速度(6/秒)，總計20輪，產量即可達到6/秒。其中入場1次，需要補19次。

如果2塔一補，2塔綠帶的產量0.597/秒，要達到黃帶速度(6/秒)，總計10輪，產量達到5.97/秒，除外入場1次，需要補9次。如果總計達到11輪，產量將是6.567/秒，超出黃帶最大接收量0.567/秒，將造成停轉。

同樣的道理，這是一個簡單的數學問題，我excel再一拉又是一個表。

由上表，我們有

1．注意標黃位置，每1、2、4、5、10、21、22塔一補氫，都算是比較劃算的。

2．如果規律補氫，我推薦10、22，畢竟安裝四向分流器也挺麻煩的。

3．11以後別補了，一補就超量。比如在13塔後面補一處氫，在第2輪的13塔處，產量早已超過黃帶容量。

可能有的吧友會問了，“唉？既然每13塔一補，黃帶會爆炸，那麼我第1輪補在13塔，第二輪隻放7座塔，這樣產出的重氫，是不是就不爆炸了？”

好問題！那麼我們進入下一個章節，不規律補氫。

本章前提：隻討論滿黃帶前隻補1次氫。

前面已經有樓層提到，“10+罐子+11可以穩定滿黃帶”，但我想說，13+8才是數值上的最優解。下面講講為什麼

當你有1個塔，其產氫期望是（1-0.99^1）*藍帶帶速

當你有2個塔，其產氫期望是（1-0.99^2）*藍帶帶速

當你要a個塔，其產氫期望是（1-0.99^a）*藍帶帶速

當***個塔，其產氫期望是（1-0.99^b）*藍帶帶速

那麼，1次補氫達到黃帶帶速，等價於某2個組合產重氫加起來等於黃帶速

（1-0.99^a）*藍帶帶速 + （1-0.99^b）*藍帶帶速 = 黃帶帶速

當你有10個塔，a=10, 即有（1-0.99^10）*藍帶帶速 + （1-0.99^b）*藍帶帶速 = 黃帶帶速

求b，一個對數運算，我們可以得到：b = 10.97

最終，a + b = 20.97 。我們需要20.97座塔，分為10塔一組、11塔一組，各1組即可達到360/m的黃帶帶速產量。

我們再給這個小系統，補上0.03座塔的額外產能，就成為前樓所說的，“10+罐子+11可以穩定滿黃帶”。當然，問題在於，0.03的額外產能，會經時間積累以後產生產物堆積。，大約40分鐘堵一次。

回到上面我們給定a的值，求b的值這一問題。這是簡單的高中數學，excel一拉又是一個表。

2次補水串聯塔總數，和首組串聯數，呈一個凹函數形態，且相對10~11附近對稱。

也就是說，串聯數為1~10的時候，總塔數遞減；串聯數11~22的時候，總塔數遞增。

藍色標記，就是“10+罐子+11可以穩定滿黃帶”；而黃色標記，8+13的組合，剛好能夠剛剛超過21塔、不溢出產能出現停轉，又不浪費產能。

這貼就差不多這樣了，主要構想就是，塔數、產出的量化，畢竟，畢竟高級傳送帶用的是孤兒產物綠馬達。

帶子沒滿載，本質上是浪費了綠馬達；帶子不夠，又浪費了轉轉樂帶子和蒸餾器。害。

最後上一個13+8、極地構建的一組簡單組合。基本350產量浮動，有過359。

構建技巧方面，合流用傳送帶左轉讓直行；分流才用四向；接入合流一小段用3級帶接入。