常見的方法有兩種：

（2.1）設定減傷上限。從圖象上看這個減傷百分比最好不要超過80%，這也是為何過去十幾年不少歐美遊戲抗性上限普遍採用70%-80%的原因。

現在我們繼續用上述圖象中的資料，分別採用0-700、0-750、0-800的資料（防禦力每10取一個資料）進行線性擬合，來看看決定系數R^2。

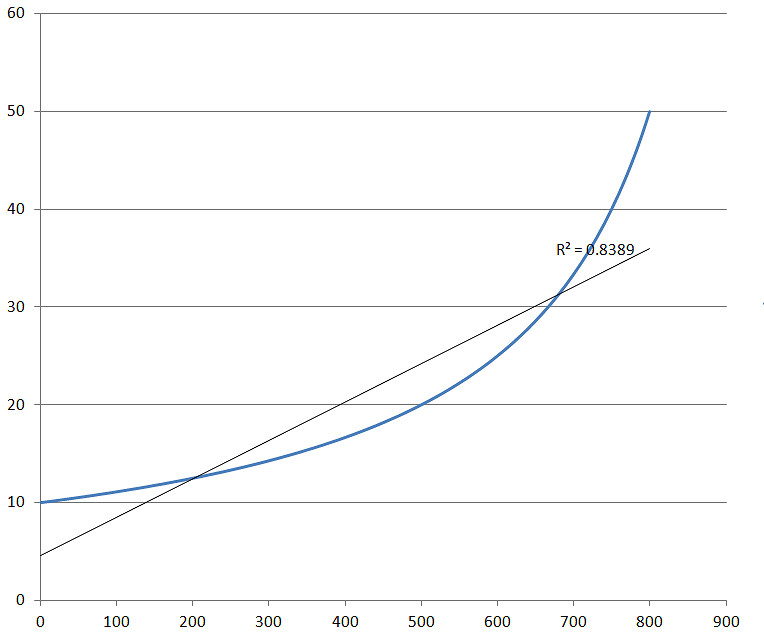
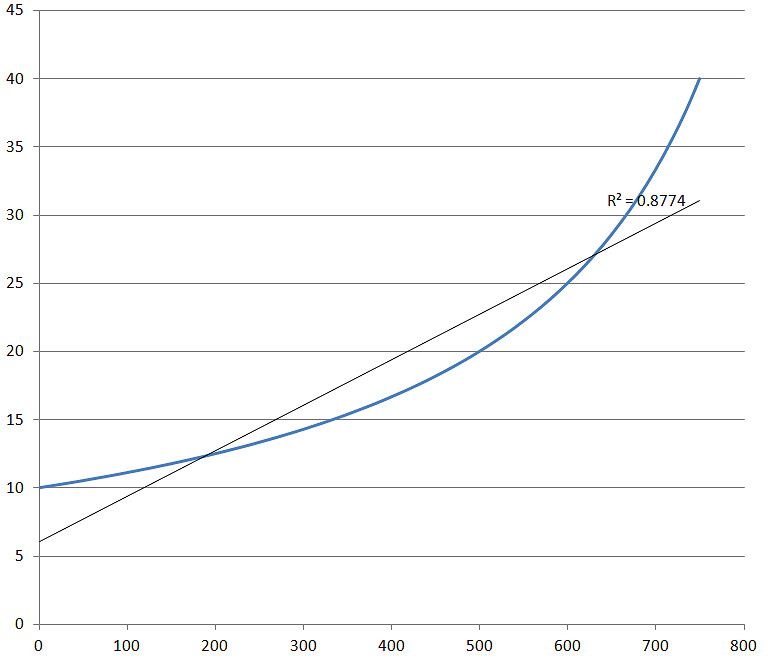
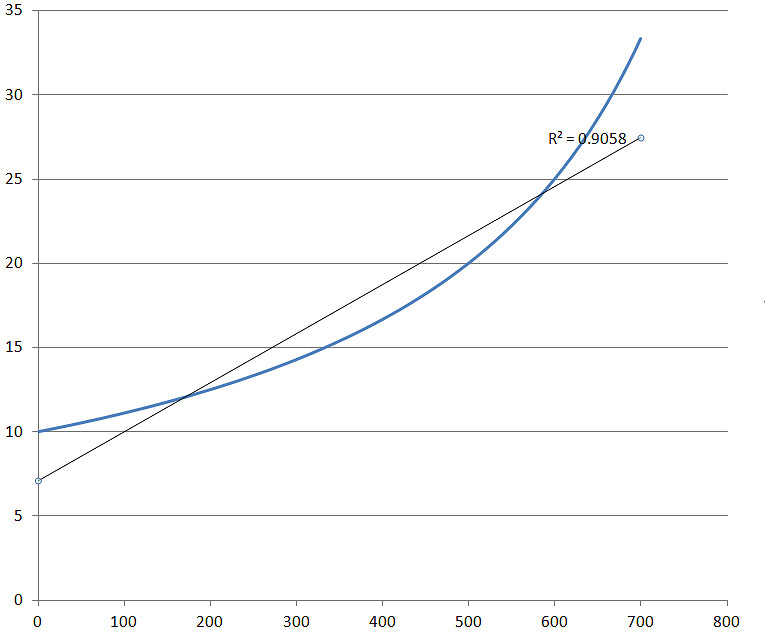
如果資料增加到900，則R^2=0.7001，下降的非常快，990的時候R^2隻有0.2305了。

（2.2）採用階梯函數。防禦力的數值越大，相應的系數就越小，以此來降低單位防禦力在數值較大時的收益。

舉例：當防禦力小於500時，減傷百分比=防禦力/1000；當防禦力大於500小於2000時，減傷百分比=50%+（防禦力-500）/5000,當防禦力大於2000時，減傷百分比=80%+（防禦力-2000）/40000。

在原始傷害=10，生命值為100的條件下，生存時間和防禦力關係的曲線圖如下（每秒攻擊一次）：

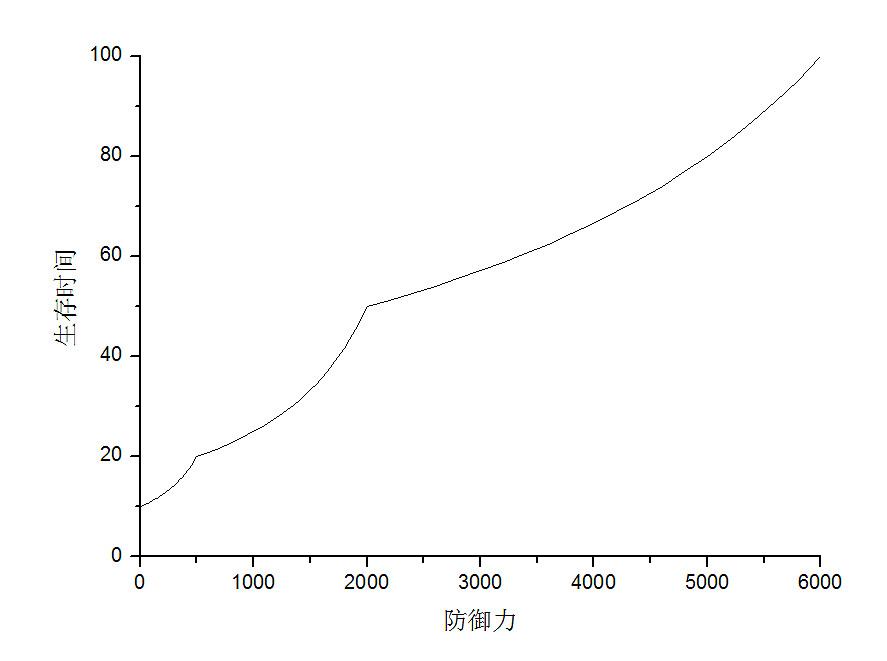
圖象上可以明顯的觀察到，只有在斷點右側單位防禦的收益會突然下降，其他所有點附近，單位防禦的收益都是單調增。用這種方法也能避免防禦收益上漲過快的問題，然而需要造一堆公式，也不是很方便。

（2.3）那麽怎樣的減傷公式才是合理的呢？從圖象分析重我們可以直觀的感受到，最好需要有一個減傷公式，使得EHP和防禦力的數值線性相關。事實上，目前的主流競技遊戲（dota2，LOL）都是採用這樣的護甲公式，以及暴雪的部分遊戲，如魔獸爭霸3、暗黑破壞神3。

令 減傷百分比 = 防禦力/（常數項+防禦力）

則 EHP = HP/（1-減傷百分比）= HP*（常數項+防禦力）/常數項

由公式可見EHP和防禦力線性相關，和（常數項+防禦力）正相關。

這樣做的好處是十分明顯的。例如我需要將一個NPC的抗擊打程度提升為原來的兩倍，只需要將（防禦力+常數項）的數值變為原來的兩倍即可，大大的節約了計算量和測試量。

來源：遊俠網